[ 목차 ]
1. 정의
2. 한정조건(예시)
3. 코드 구현
4. 정리
▶ 백트래킹(Back Tracking) : 퇴각 검색
- 한정조건에서의 모든 경우의 수를 탐색하는 알고리즘
- 전체 조건에서 모든 경우의수를 탐색하는 완전탐색 (≒ 브루트 포스) 알고리즘보다 빠른 탐색이 가능하다.
- 어떤 지점이 한정조건에 부합하지 않음이 명백할 경우, 이전 지점으로 돌아가며 다른 지점을 다시 탐색하는 방식으로 작동.
- 위 작동 방식 때문에 이전에 알아본 DFS를 이용한 탐색이 선호됨 (깊이 우선 탐색)
◈ 한정조건 (예시)
백트래킹과 한정조건에 대한 이해를 돕기 위해 백준 9663번 N-Queen 문제를 들고왔다.
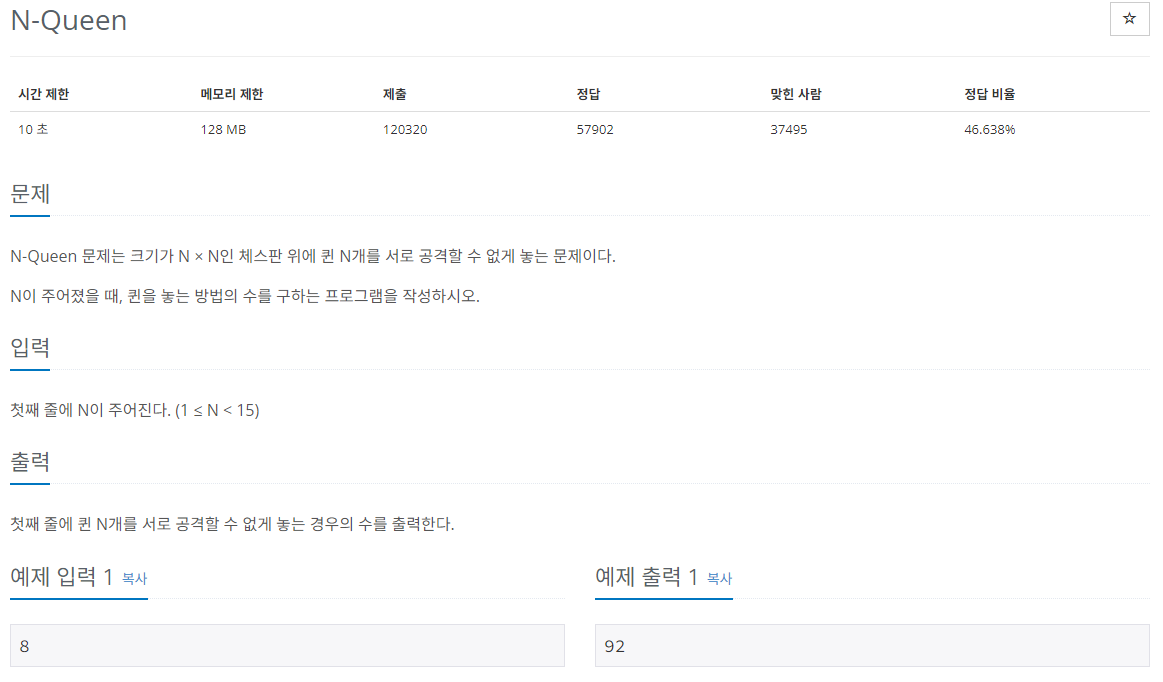
문제 힌트에 있는 Queen - The show must go on을 들으며 풀어보자(...)
우선, 이 문제의 한정조건은 N개의 퀸을 서로 공격할 수 없게 놓는다는 것이다. 체스를 해본 사람이라면 알겠지만, 퀸은 자신과 같은 행, 열, 모든 대각선으로 이동할 수 있기 때문에, 서로 공격할 수 없게 놓는다는 것은 같은 열, 행, 대각선에 아무런 기물이 없어야 함을 의미한다.
따라서 우리는 각 행마다 퀸을 놓는 방식으로, 같은 열과 대각선에 기물이 있는지 없는지를 판별하며 백트래킹을 구현할 것이다.
처음 탐색하는 경우) 행 우선
| Q | x | x | x |
| x | x | ||
| x | x | ||
| x | x |
| Q | x | x | x |
| x | x | Q | x |
| x | x | x | x |
| x | x | x |
| Q | x | x | x |
| x | x | Q | x |
| x | x | x | x |
| x | x | x |
3번째 열이 비어있지 않으므로 if문이 돌아가지 않음. (1열까지 백트래킹)
static int count = 0; // 퀸을 놓는 방법의 수
static boolean[] col_IsEmpty = new boolean[15]; // 각 열에 퀸이 놓여 있는지 여부
static boolean[] ang1_IsEmpty = new boolean[29]; // 대각선 1 ( / 방향 )
static boolean[] ang2_IsEmpty = new boolean[29]; // 대각선 2 ( \ 방향 )
백트래킹을 실행하는 메서드는 DFS방식을 사용하기 때문에, 재귀를 이용하여 구현한다.
public static void DFS(int row, int n) {
if (row == n) {
count++; // 모든 퀸을 놓았을 때 경우의 수 증가
return;
}
for (int col = 0; col < n; col++) {
if (!col_IsEmpty[col] && !ang1_IsEmpty[row + col] && !ang2_IsEmpty[row - col + n - 1]) {
// 현재 열과 두 대각선이 비어 있으면 퀸을 놓는다
col_IsEmpty[col] = true;
ang1_IsEmpty[row + col] = true;//(row,col)의 좌표에 대한 오른쪽 위 대각선이라고 생각하면 편하다
ang2_IsEmpty[row - col + n - 1] = true;// 오른쪽 아래 대각선
DFS(row + 1, n); // 다음 행으로 이동
/*
백트래킹 할 부분
*/
}
}
}
이제 재귀 이후에 백트래킹 부분을 구현해주어야 하는데, 재귀 메서드가 베이스케이스를 찍어 COUNT를 1 증가시키고 재귀호출이 끝났을 때 이미 퀸이 놓여있기 때문에, 바꿔말하면 기물의 위치를 판별할 IsEmpty 배열들이 채워져 있기 때문에, 백트래킹을 하기 위해 재귀 이후에는 이미 채워진 배열의 인덱스를 초기화한다.
처음 탐색하는 경우 이후 코드 진행 순서)
1) 퀸 삭제(백트래킹) (현재 반복문 탐색 위치 P)
| x | P | ||
1-2) P의 위치에 퀸을 놓고, 반복문의 끝까지 다시 탐색(DFS)
| x | Q | x | x |
| x | x | x | Q |
| Q | x | x | x |
| x | x | Q | x |
1-3) 베이스 케이스를 만족했으므로 카운트 증가. 리턴 후 재귀 종료 (다음 케이스 백트래킹 시작)
2) 1)의 P위치에서 한 칸 이동한 후, 퀸을 놓고 이후 반복.
// 퀸을 다시 제거 (백트래킹)
col_IsEmpty[col] = false;
ang1_IsEmpty[row + col] = false;
ang2_IsEmpty[row - col + n - 1] = false;
전체 코드는 아래와 같다.
import java.util.Scanner;
public class BackTracking {
static int count = 0; // 퀸을 놓는 방법의 수
static boolean[] col_IsEmpty = new boolean[15]; // 각 열에 퀸이 놓여 있는지 여부
static boolean[] ang1_IsEmpty = new boolean[29]; // 대각선 1 ( / 방향 )
static boolean[] ang2_IsEmpty = new boolean[29]; // 대각선 2 ( \ 방향 )
public static void DFS(int row, int n) {
if (row == n) {
count++; // 모든 퀸을 놓았을 때 경우의 수 증가
return;
}
for (int col = 0; col < n; col++) {
if (!col_IsEmpty[col] && !ang1_IsEmpty[row + col] && !ang2_IsEmpty[row - col + n - 1]) {
// 현재 열과 두 대각선이 비어 있으면 퀸을 놓는다
col_IsEmpty[col] = true;
ang1_IsEmpty[row + col] = true;//(row,col)의 좌표에 대한 오른쪽 위 대각선이라고 생각하면 편하다
ang2_IsEmpty[row - col + n - 1] = true;// 오른쪽 아래 대각선
DFS(row + 1, n); // 다음 행으로 이동
// 퀸을 다시 제거 (백트래킹)
col_IsEmpty[col] = false;
ang1_IsEmpty[row + col] = false;
ang2_IsEmpty[row - col + n - 1] = false;
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt(); // N 입력받기
DFS(0, n); // 첫 번째 행부터 시작
System.out.println(count); // 경우의 수 출력
}
}
▶출력 결과


▶정리
- 백트래킹은 한정조건에서의 모든 경우의 수를 탐색하는 알고리즘
- 완전탐색 (≒ 브루트 포스) 알고리즘보다 빠른 탐색이 가능하다.
- DFS를 이용한 탐색이 선호됨 (깊이 우선 탐색)
퀸은 전설이다
'모각코' 카테고리의 다른 글
| [알고리즘] 그리디 알고리즘(탐욕법, Greedy Algorithm) 이해하기 (0) | 2024.08.04 |
|---|---|
| [알고리즘] 다익스트라 (데이크스트라, Dijkstra) 이해하기 (0) | 2024.07.29 |
| [알고리즘] 브루트 포스(Brute Force) 이해하기 (1) | 2024.07.21 |
| [알고리즘] 다이나믹 프로그래밍(Dynamic Programming) 이해하기 (1) | 2024.07.20 |
| [알고리즘] DFS(깊이 우선 탐색)와 BFS(넓이 우선 탐색) 이해하기 (0) | 2024.07.05 |



