[ 목차 ]
1.정의
1-1.DFS (Depth-First Search)
1-2.BFS (Breadth-First Serch)
2.구현
2-1.DFS의 구현 방법
2-2.BFS의 구현 방법
3.DFS의 재귀
4.코드 구현(전체 코드 미리보기)
4-1.Stack으로 구현한 DFS
4-2.Queue로 구현한 BFS
4-3.재귀로 구현한 DFS
4-4.출력 결과
5.정리
▶ DFS (Depth-First Search)
- 그래프 검색에 사용된다.
- 이진트리에서 사용했던 PreOrder, InOrder, PostOrder 순회방법
- Stack 자료구조를 이용하여 구현한다.
▶ BFS (Breadth-First Search)
- 마찬가지로 그래프 검색에 사용.
- 이진트리에서 사용했던 LevelOrder 순회 방법
- Queue 자료구조를 이용하여 구현한다.
▶ DFS의 구현 방법
1. 최초 탐색 시작 시, 노드를 스택에 삽입하고 방문처리
2. 스택 최상단에 있는 노드의 인접노드를 모두 방문했는지 확인한다.
2-1. 방문하지 않은 노드가 있다면 그 노드들을 스택에 넣고 방문처리
2-2. 모든 노드를 방문했다면 최상단에 있는 노드를 제거.
3. 2의 과정을 수행할수 없을 때 까지 반복.
예시 출처 : [자료구조 알고리즘] Graph 검색 DFS, BFS 구현 in Java
https://youtu.be/_hxFgg7TLZQ?si=RXZFcGPypRe0pb0Y

위 예시에서 DFS의 순회 순서는 (시작 노드가 0일 때)
0 > 1 > 3 > 5 > 7 > 6 > 8 > 4 > 2
▶ BFS의 구현방법
1. 최초 탐색 시작 시, 노드를 큐에 삽입하고 방문처리
2. 큐의 최상단 노드를 꺼내고, 해당 노드와 인접한 모든 노드 삽입 후 방문처리
3. 2의 과정을 수행할수 없을 때 까지 반복.

위 예시에서 DFS의 순회 순서는 (시작 노드가 0일 때)
0 > 1 > 2 > 3 > 4 > 5 > 6 > 7 > 8
참고) 큐는 FIFO, 스택은 LIFO
▶ DFS의 재귀
- 둘 중 DFS는 재귀로 구현하면 매우 간결한 코드로 구현할 수 있다.
- 사용자가 미리 설정해둔 순서대로 자식노드들을 호출하며 방문처리를 하는 방식.

★★ 스택을 사용한 DFS구현과의 다른 점 ★★
- LIFO인 스택과 달리, FIFO방식으로 2가 먼저 출력
- 우선순위 구현 방식에 따라, 3이 4의 자식이 될 수도 있음
▶코드 구현 (전체 코드 미리보기)
import java.util.*;
class Graph{ //그래프 생성
class Node{ //노드 정의
int data; //편의상 데이터는 정수형으로 받음
LinkedList<Node> a; //리스트 형식을 따름
boolean marked; //방문표시를 위한 boolean
Node (int data) {
this.data = data;
this.marked = false; //false로 초기화
a = new LinkedList<Node>();
}
}
Node[] nodes;
Graph(int size){//그래프 size 임의 설정
nodes = new Node[size];
for(int i = 0; i< size; i++) {
nodes[i] = new Node(i);
}
}
void addEdge(int i1, int i2) { //두 노드를 연결하는 함수
Node n1 = nodes[i1];
Node n2 = nodes[i2];
if(!n1.a.contains(n2)) { //두 노드가 연결되어있는지 확인
n1.a.add(n2); //두 노드를 연결
}
if(!n2.a.contains(n1)) {
n2.a.add(n1);
}
}
void stackDfs(int index) { //스택을 이용한 DFS구현
Node root = nodes[index];
Stack<Node> stack = new Stack<Node>();
stack.push(root);
root.marked = true;
while(!stack.isEmpty()) {
Node p = stack.pop();
for(Node n : p.a) {
if (n.marked == false) {
n.marked = true;
stack.push(n);
}
}
visit(p); //p를 출력하는 함수
}
}
void queueBfs(int index) { //큐를 이용한 BFS구현
Node root = nodes[index];
Queue<Node> queue = new LinkedList<Node>();
queue.add(root);
root.marked = true;
while(!queue.isEmpty()) {
Node p = queue.remove();
for(Node n: p.a) {
if (n.marked == false) {
n.marked = true;
queue.add(n);
}
}
visit(p);
}
}
void recDfs(Node p) { //재귀로 DFS구현
if (p == null) return;
p.marked = true;
visit(p); //재귀 전에 미리 출력
for(Node n : p.a) {
if(n.marked == false) {
recDfs(n);
}
}
}
void recDfs(int index) { //index로 받아서 구현
Node p = nodes[index];
recDfs(p);
}
void visit(Node n) {
System.out.print(n.data + " ");
}
}
public class Main{
public static void main (String[] args){
Graph g = new Graph(9); //그림과 같은 관계 구현
g.addEdge(0, 1);
g.addEdge(1, 2);
g.addEdge(1, 3);
g.addEdge(2, 4);
g.addEdge(2, 3);
g.addEdge(3, 4);
g.addEdge(3, 5);
g.addEdge(5, 6);
g.addEdge(5, 7);
g.addEdge(6, 8);
g.stackDfs(0);
//g.queueBfs(0);
//g.recBfs(0);
}
}
▶코드 구현 (Stack으로 구현한 DFS)
void stackDfs(int index) { //스택을 이용한 DFS구현
Node root = nodes[index];
Stack<Node> stack = new Stack<Node>(); //스택 불러오기
stack.push(root);
root.marked = true;
while(!stack.isEmpty()) {
Node p = stack.pop();
for(Node n : p.a) { //노드p와 연결되어있는 모든 노드들을 순회
if (n.marked == false) { //방문한 적이 없으면
n.marked = true; //방문처리 후
stack.push(n); //스택에 삽입
}
}
visit(p); //p를 출력하는 함수
}
}
- 핵심 부분은 for문과 그 내부
- 노드p에 LinkedList로 연결된 노드들을 순회하며 방문여부를 확인 후 스택에 삽입
▶코드 구현 (Queue로 구현한 BFS)
void queueBfs(int index) { //큐를 이용한 BFS구현
Node root = nodes[index];
Queue<Node> queue = new LinkedList<Node>();
queue.add(root);
root.marked = true;
while(!queue.isEmpty()) {
Node p = queue.remove();
for(Node n: p.a) {
if (n.marked == false) {
n.marked = true;
queue.add(n);
}
}
visit(p);
}
}- Stack이 아닌 Queue 자료구조를 사용
- 코드 구조는 stackDfs와 동일
▶코드 구현 (Recursion으로 구현한 DFS)
void recDfs(Node p) { //재귀로 DFS구현
if (p == null) return;
p.marked = true;
visit(p); //재귀 전에 미리 출력
for(Node n : p.a) {
if(n.marked == false) {
recDfs(n);
}
}
}
void recDfs(int index) { //index로 받아서 구현
Node p = nodes[index];
recDfs(p);
}- 위의 두 메서드보다 훨씬 간결한 코드
- for문을 사용한다는 점에서는 위 두 코드와 구조가 유사.
▶출력 결과
◈ 스택으로 구현한 DFS

◈ 큐로 구현한 BFS

◈ 재귀로 구현한 DFS
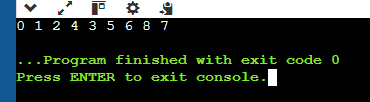
▶정리
- DFS와 BFS는 선으로 복잡하게 얽힌 관계에서 탐색을 시도하는 알고리즘
- DFS는 스택과 재귀로, BFS는 큐로 구현할 수 있음
- DFS는 코드의 가독성을 위해 재귀로 구현하는것이 효과적. (때에 따라 다름)
- java를 사용한 코드 구현에서 노드를 LinkedList로 연결하여 관계를 선언하는 것이 효과적.
'모각코' 카테고리의 다른 글
| [알고리즘] 그리디 알고리즘(탐욕법, Greedy Algorithm) 이해하기 (0) | 2024.08.04 |
|---|---|
| [알고리즘] 다익스트라 (데이크스트라, Dijkstra) 이해하기 (0) | 2024.07.29 |
| [알고리즘] 백트래킹(Back Tracking) 이해하기 (0) | 2024.07.28 |
| [알고리즘] 브루트 포스(Brute Force) 이해하기 (1) | 2024.07.21 |
| [알고리즘] 다이나믹 프로그래밍(Dynamic Programming) 이해하기 (1) | 2024.07.20 |



